Genrerating contact points for AMASS dataset

AMASS is a huge motion library

AMASS is a massive motion library for the SMPL body model. More information about AMASS and SMPL are here and here respectively. Few examples are shown below:

Which contact points do we want?

We are interested in the contact of the mesh with the static environment where the static friction is acting during the motion. An example of such contacts is the foot contacts with the ground when a person is walking. It does not include the self contact of the person e.g. contact of two hands while clapping. It also does not include the contact with the objects in the environment which can be moved by the person e.g. a mug.

Let's calculate the contact probabilities

We calculate the probabilities of each joint/vertex being in contact at every frame. We hypothesize that:

• If a joint is in contact then its velocity at that time instant will be zero.

• Vertically lower joints are more probable of being in contact.

The probability of joint $j$ being in contact can be given as

,

where $p(v_j)$ and $p(z_j)$ are the contact probability of joint $j$ given its velocity $v_j$ and height from the lowest point og the body $z_j$.

If the joint has a non-zero velocity, its contact probability is close to $0$. We can model $p(v_j)$ as

.

We model the $p(z_j)$ as

Let us have a look how these models look like

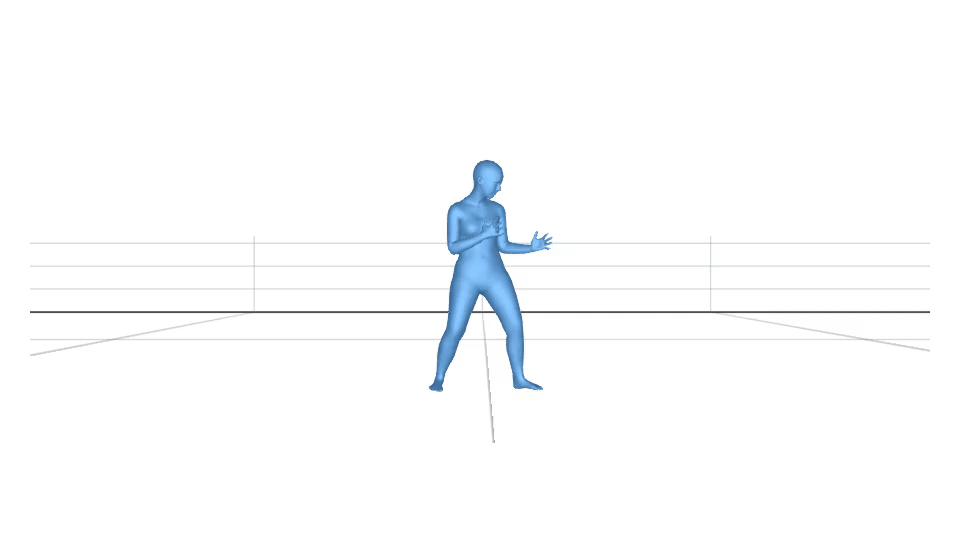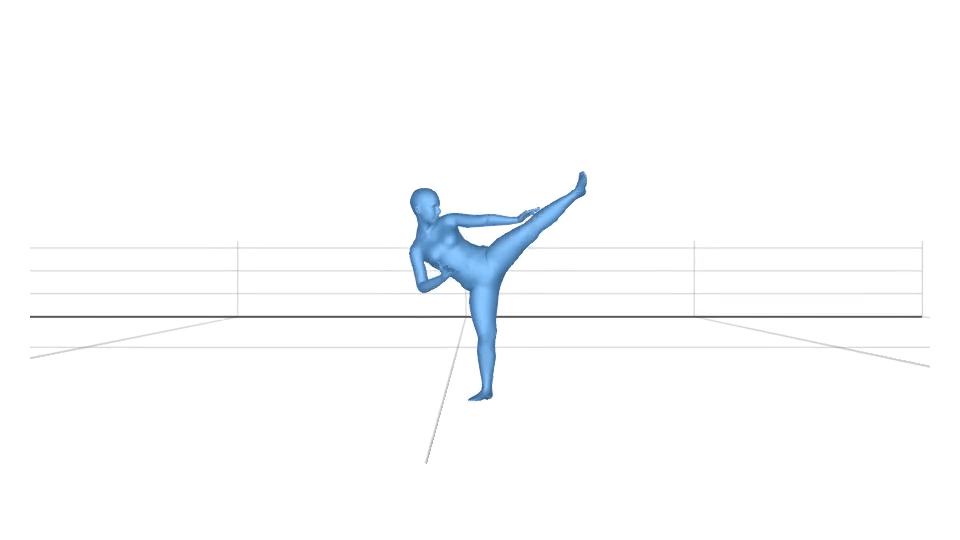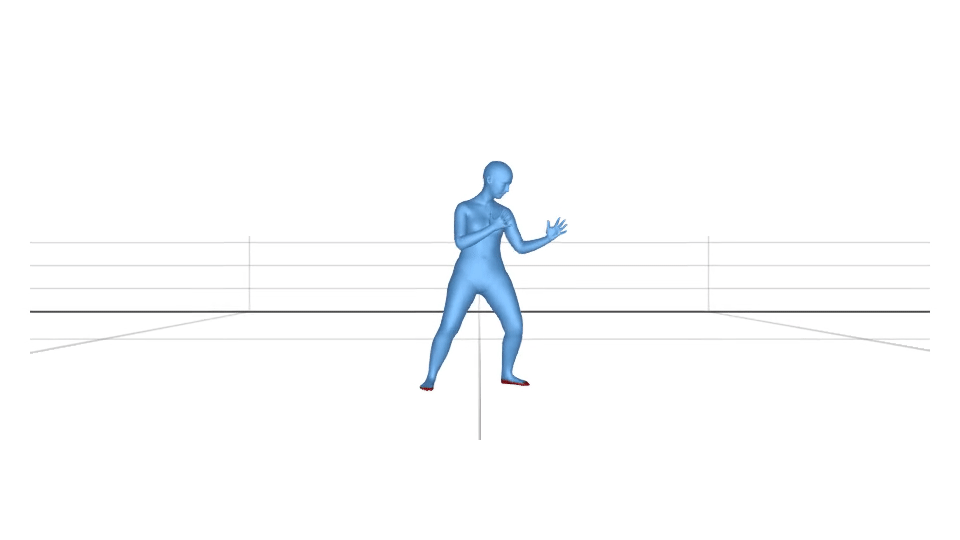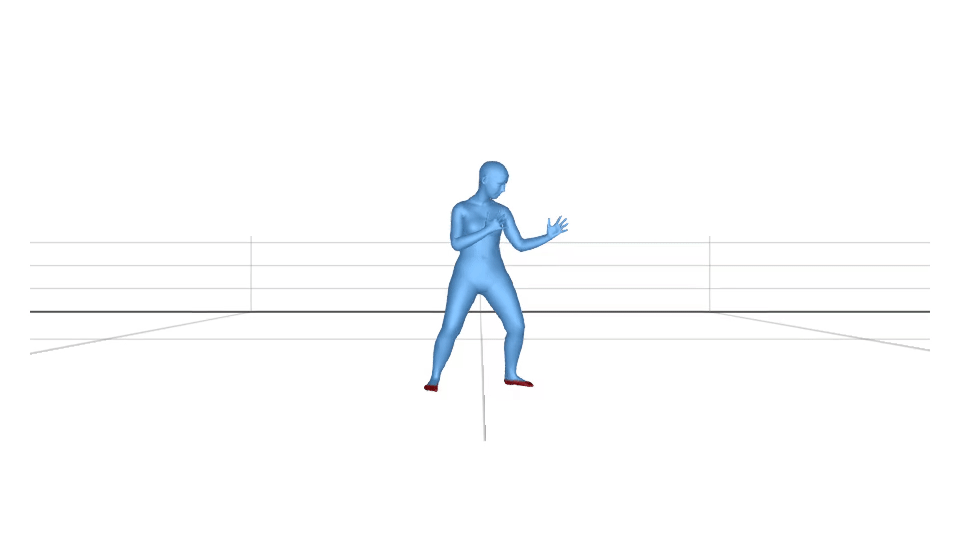
Using equation (1), we visualize the body joints which are in contact. The sphere radius and the colour depends on the value of $p_j$. The higher value corresponds to the bigger sphere radius.

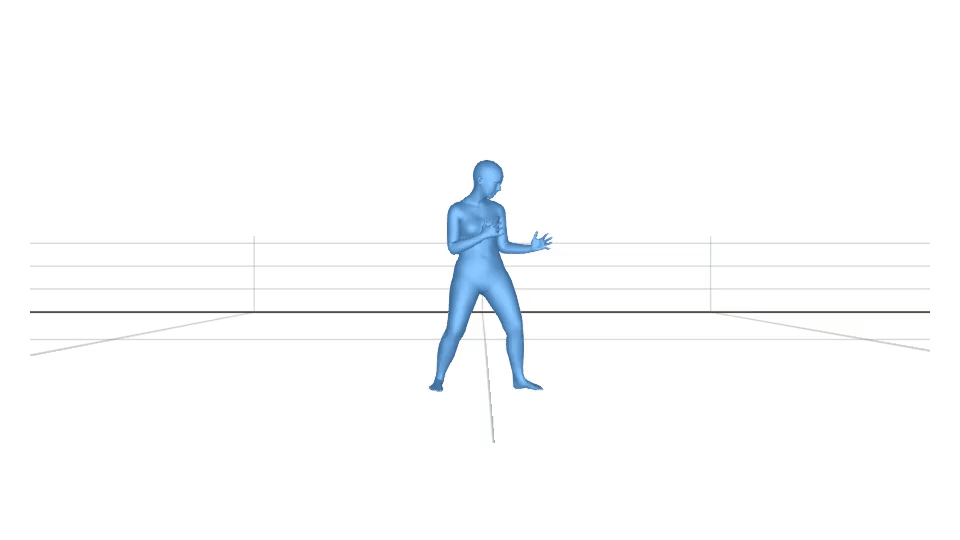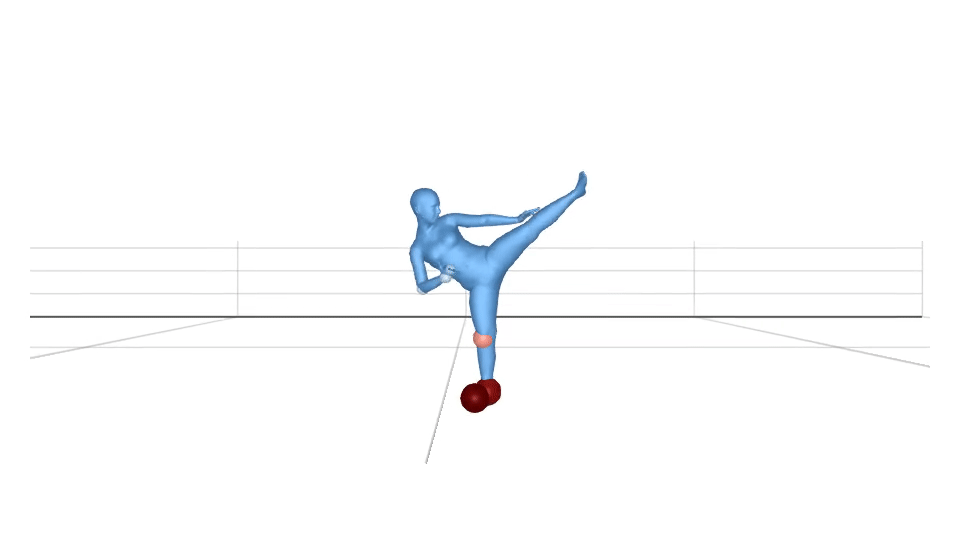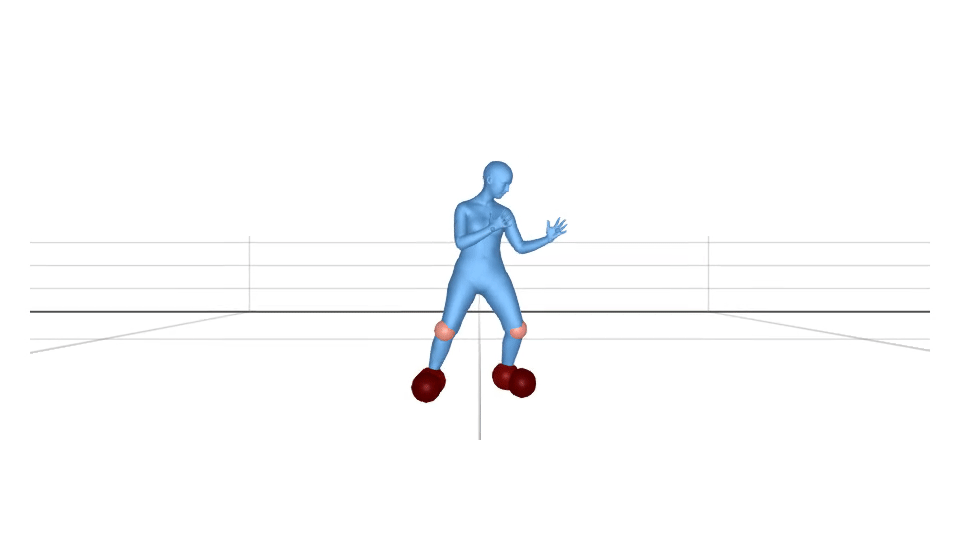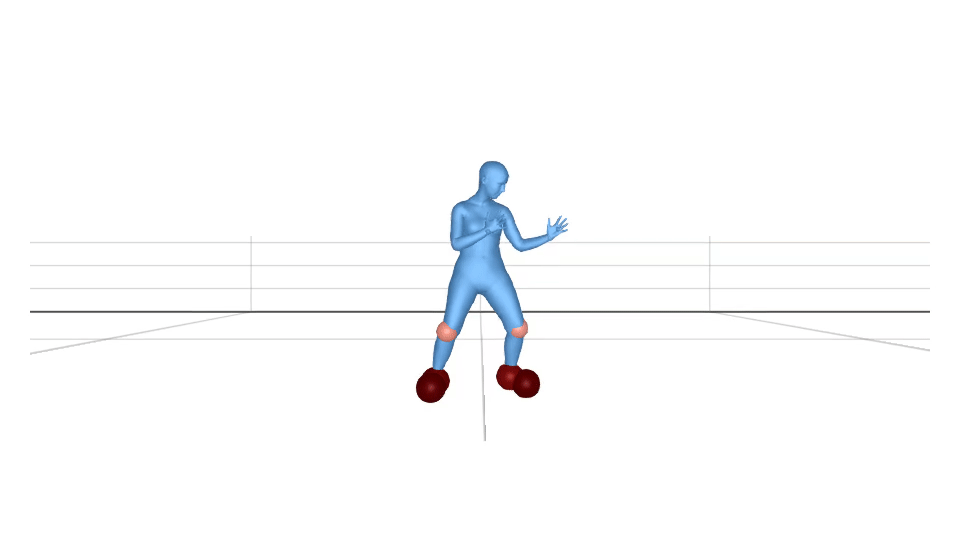
We can clip the $p_j$ values to $0$ if they are less than a threshold value. If we fix the threshold value to be $0.95$, the visualization looks like this.

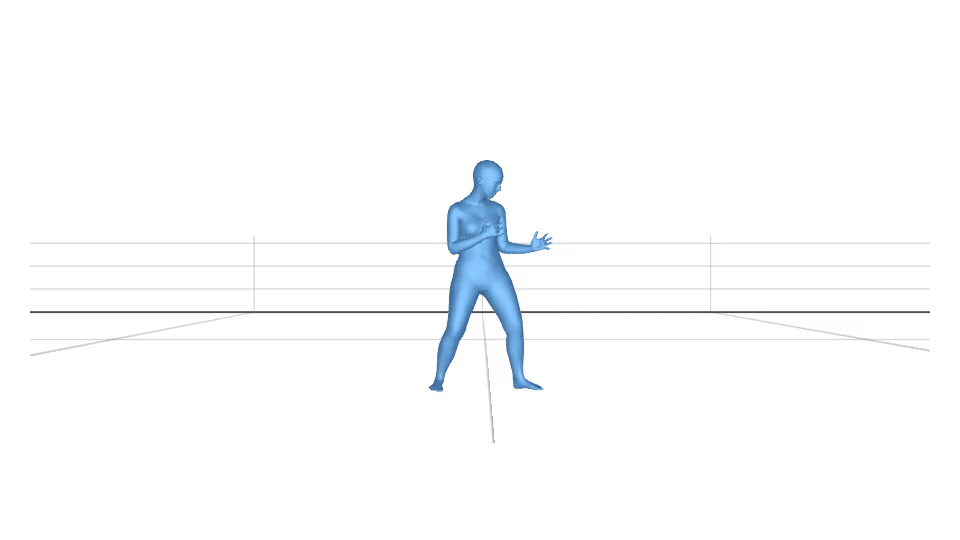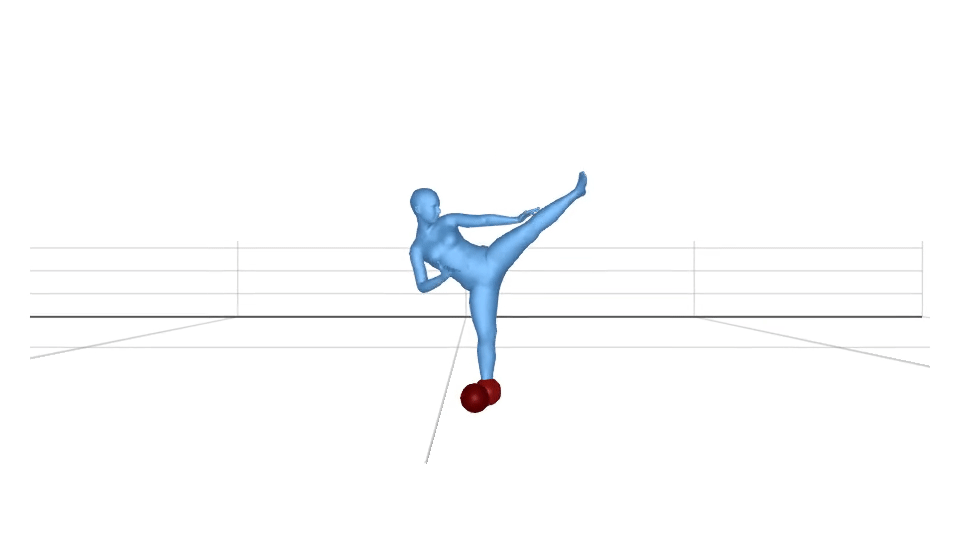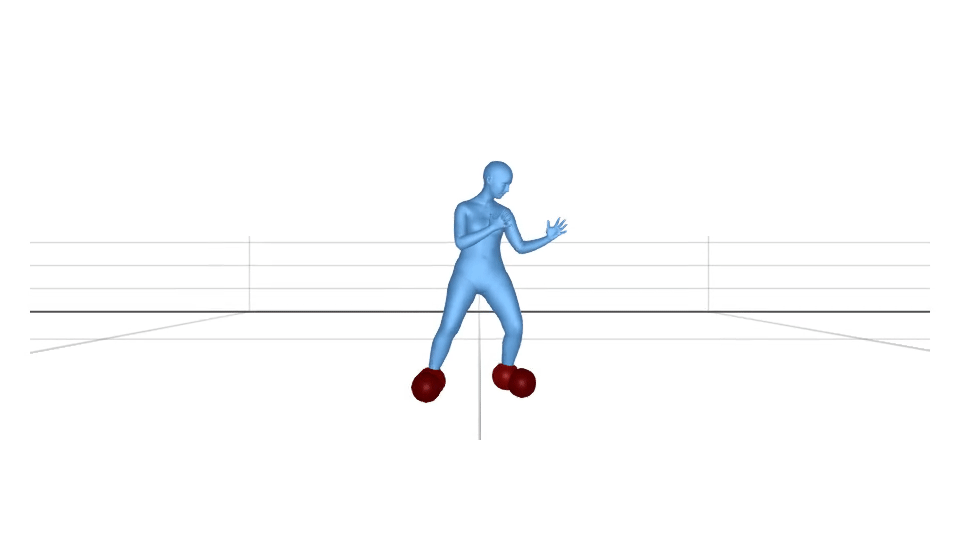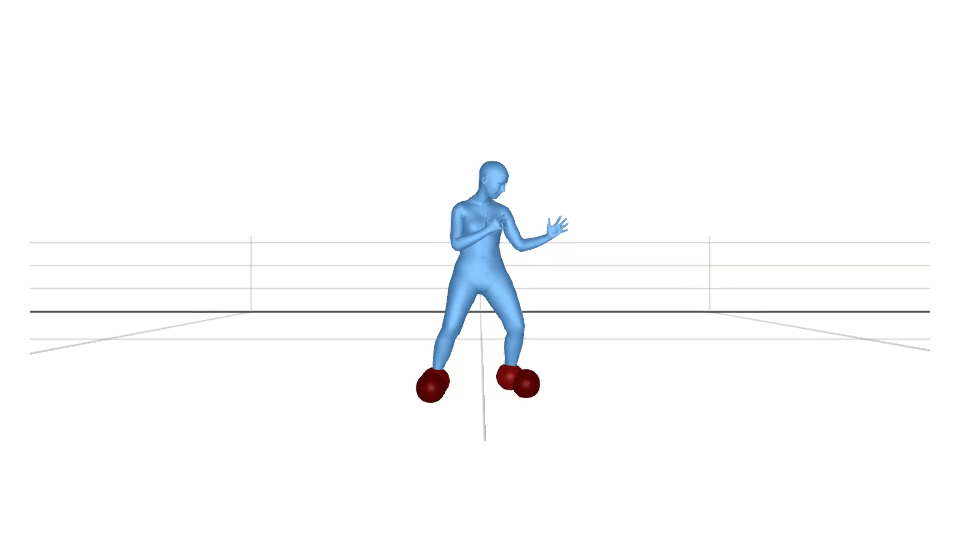
In the real world, the body surface gets in contact with the environment, not the body joints. Let us use the above-mentioned method for the body vertices. We calculate $p_v$ instead of $p_j$ in the same way as $p_j$. The visualization looks like this.

The code is not publicly available, however, it is available upon request.